머신러닝 공부 - 로지스틱 회귀(Logistic Regression) 쉽게 이해하기

머신러닝에서 2진 분류(Binary Classification) 모델로 사용되는 로지스틱 회귀 알고리즘에 대한 개념을 최대한 쉽게 소개한다. (이전에 선형회귀에 대한 개념을 알고 있다면 금방 이해할 수 있는 수준으로 작성했다.)

로지스틱 회귀란 무엇인가

로지스틱 회귀(Logistic Regression)는 회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘이다.

스팸 메일 분류기 같은 예시를 생각하면 쉽다. 어떤 메일을 받았을 때 그것이 스팸일 확률이 0.5 이상이면 spam으로 분류하고, 확률이 0.5보다 작은 경우 ham으로 분류하는 거다. 이렇게 데이터가 2개의 범주 중 하나에 속하도록 결정하는 것을 2진 분류(binary classification)라고 한다.

로지스틱 회귀를 이해하려면 우선 선형 회귀(Linear Regression)에 대한 개념을 먼저 익혀야 한다.

예를 들어 어떤 학생이 공부하는 시간에 따라 시험에 합격할 확률이 달라진다고 해보자. 선형 회귀를 사용하면 아래와 같은 그림으로 나타낼 수 있다.

공부한 시간이 적으면 시험에 통과 못하고, 공부한 시간이 많으면 시험에 통과한다는 식으로 설명할 수 있다. 그런데 이 회귀선을 자세히 살펴보면 확률이 음과 양의 방향으로 무한대까지 뻗어 간다. 말 그대로 ‘선’이라서. 그래서 공부를 2시간도 안 하면 시험에 통과할 확률이 0이 안 된다. 이건 말이 안 된다.

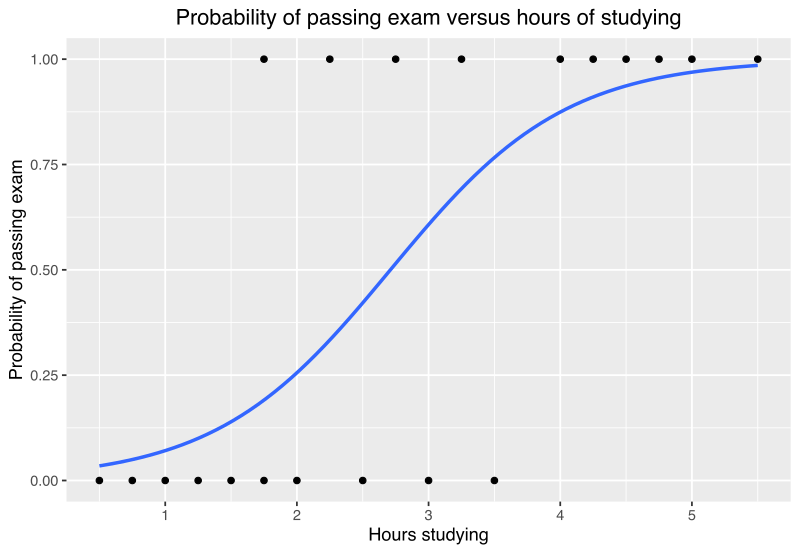
만약 로지스틱 회귀를 사용하면 아래와 같이 나타난다.

시험에 합격할 확률이 0과 1사이의 값으로 그려진다. 이제야 좀 납득이 된다.

로지스틱 회귀에서는 데이터가 특정 범주에 속할 확률을 예측하기 위해 아래와 같은 단계를 거친다.

1. 모든 속성(feature)들의 계수(coefficient)와 절편(intercept)을 0으로 초기화한다.
2. 각 속성들의 값(value)에 계수(coefficient)를 곱해서 log-odds를 구한다.
3. log-odds를 sigmoid 함수에 넣어서 [0,1] 범위의 확률을 구한다.

어려워서 이해가 안 되도 된다. 차근차근 뒤에서 다시 설명하겠다.

Log-Odds

선형 회귀에서는 각 속성의 값에다가 계수(coefficient)에 각 곱하고 절편(intercept)을 더해서 예측 값을 구한다. 그래서 구한 예측 값의 범위는 -∞에서 + ∞까지다. 로지스틱 회귀에서도 마찬가지이긴 한데, 마지막에 예측 값 대신 log-odds라는 걸 구해줘야 한다는 차이가 있다.

log-odds를 어떻게 구하는지 알려면 일단 odds부터 계산해야 하는데, 사건이 발생할 확률을 발생하지 하지 않을 확률로 나눈 값이다.

Odds = 사건이 발생할 확률 / 사건이 발생하지 않을 확률

그래서 만약 학생이 0.7 확률로 시험에 합격한다면, 당연히 시험에서 떨어질 확률은 0.3이 되니까 odds는 0.7 / 0.3이 된다. 그리고 이렇게 구한 odds에 log를 취한 것이 바로 log-odds다. 일단 개념은 쉽다.

그런데 로지스틱 회귀에서는 아래와 같이 여러 속성(feature)들에 계수(coefficient)를 곱하고 절편(intercept)을 더해서 최종 값 log-odds를 구해야 하기 때문에 좀 까다롭다.

그래서 여기서는 (‘내적’ 혹은 ‘점곱’이라고 부르는) dot product 방식으로 log-odds를 구한다.

일단 각 속성(feature)들의 값이 포함된 행렬, 그 속성들 각각의 계수(coefficient)가 포함된 행렬을 아래와 같이 계산할 수 있다.

log_odds = np.dot(features, coefficients) + intercept

 

Sigmoid Function

로지스틱 회귀에서는 (위에서 잠깐 보여준 것과 같이) 확률을 0에서 1사이로 커브 모양으로 나타내야 하는데, 이걸 가능하게 해주는 게 바로 Sigmoid 함수다.

\[f(x)={\frac {1}{1+e^{-z}}}\]

위에서 구한 log-odds를 Sigmoid 함수에 넣어서 0부터 1사이의 값으로 변환해주는 거다.

여기서 e^(-z)는 지수 함수이고, numpy에서 np.exp(-z)로 쉽게 계산할 수 있다.

Log Loss (로그 손실)

로지스틱 회귀가 확률을 제대로 예측해주는지, 즉 구해놓은 속성들의 계수(coefficients)와 절편(intercept)이 적절한지 확인하기 위해 손실(Loss)을 고려해야 한다. 이전에도 선형회귀에서도 손실 함수(Loss Function)에 대한 개념을 설명한 바 있다.

아무튼 모델의 “적합성”을 평가하기 위해 각 데이터 샘플의 손실(모델 예측이 얼마나 잘못되었는지)을 계산한 다음 그것들의 평균화 해야 한다.

로지스틱 회귀에 대한 손실 함수는 Log Loss(로그 손실)라고 부르며, 아래와 같이 구할 수 있다.

\[-\frac{1}{m}\sum_{i=1}^m [y^{(i)} log(h(z^{(i)})) + (1-y^{(i)}) log(1 - h(z^{(i)}))]\]

• m:데이터 총 개수
• y_i: 데이터 샘플 i의 분류
• z_i: 데이터 샘플 i의 log-odd
• h(z_i): 데이터 샘플 i의 log-odd의 sigmoid (즉, 데이터 샘플 i가 분류에 속할 확률)

어려워보이긴 하는데, 뭐 다 이해 못해도 괜찮다. (사실 나도 깊이 들어가면 잘 모른다.) 어쨌거나 로지스틱 회귀 모델의 목표는 로지스틱 함수를 구성하는 계수와 절편에 대해 Log Loss(로그 손실)을 최소화하는 값을 찾는 것이라고 이해하자.

그런데 이 로그 손실을 두 개로 나눠서 이해할 필요가 있다. 왜냐면 로지스틱 회귀는 특정 범주로 분류될 것인가, 그렇지 않을 것인가, 즉 2진 분류를 하기 때문에.

어떤 데이터 샘플의 클래스 y=1 인 경우, 즉 학생이 시험에 합격한 경우에 손실은 아래와 같이 계산된다.

\[- log(h(z^{(i)}))\]

이 데이터의 손실은 그냥 학생이 시험에 통과할 확률에 로그를 씌운 것밖에 안 된다. (식이 어려우면 그냥 개념적으로만 이해해도 된다.)

반대로 y=0, 즉, 학생이 시험에 탈락한 경우는 손실이 아래와 같이 계산된다.

\[- log(1 - h(z^{(i)}))\]

이 데이터의 손실도 그냥 학생이 시험에 탈락할 확률을 1에서 빼고 로그를 씌운 것뿐이다.

결국 분류(레이블)가 y=1,y=0 일 때 각각의 손실 함수를 그래프로 나타내면 아래와 같다.

정확한 예측은 손실이 거의 없는 반면 잘못된 예측은 거의 무한대에 가까운 큰 손실을 초래하는 꼴이다. (뭐 당연한 거다. 시험 공부 거의 안 한 학생이 시험에 붙을 확률은 0에 가까우니까.)

아무튼 이렇게 예측이 잘못되면서 손실이 점진적으로 증가하는 꼴을 줄이고, 올바른 예측을 하면서 손실이 작아지는 모델에 가까워지도록 하는 게 우리의 목표가 될 거다. 그래서 선형 회귀와 마찬가지로 경사하강법(Gradient Descent)을 사용하여 모든 데이터에서 로그 손실(Log Loss)을 최소화하는 계수를 찾을 수 있다.

Threshold (임계값)

로지스틱 회귀 알고리즘의 결과 값은 ‘분류 확률’이고, 그래서 이 확률이 특정 수준 이상 확보되면 샘플이 그 클래스에 속할지 말지 결정할 수 있다.

그리고 당연히 대부분의 알고리즘에서 기본 임계 값은 0.5다. 다만, 필요에 따라 모델의 임계값을 변경할 수 있다.

예를 들어, 암을 진단하는 로지스틱 회귀 모델을 작성하는 경우에는 혹시 모를 경우에 대비하여 좀 더 민감하게 확인하기 위해 0.3이나 0.4로 임계값을 낮춰 모델의 민감도를 높일 필요가 있다. 그래야 전체적으로 오분류가 더 많아지더라도 실제 암 환자를 놓치는 사례는 적어질 테니까.

아래 그림으로 이해해보자.

만약, 0.5 임계값인 경우에는 이런 꼴이지만

0.4의 임계값으로 조정하면 이렇게 된다.

요약

• 로지스틱 회귀 분석은 이진 분류를 수행하는 데 사용된다. 즉, 데이터 샘플을 양성(1) 또는 음성(0) 클래스 둘 중 어디에 속하는지 예측한다.
• 각 속성(feature)들의 계수 log-odds를 구한 후 Sigmoid 함수를 적용하여 실제로 데이터가 해당 클래스에 속할 확률을 0과 1사이의 값으로 나타낸다.
• 손실함수(Loss Function)는 머신러닝 모델이 얼마나 잘 예측하는지 확인하는 방법이다. 로지스틱 회귀의 손실함수는 Log Loss이다.
• 데이터가 클래스에 속할지 말지 결정할 확률 컷오프를 Threshold(임계값)이라 한다. 기본 값은 0.5이지만 데이터의 특성이나 상황에 따라 조정할 수 있다.
• 파이썬 라이브러리 Scikit-learn을 통해 모델을 생성하고 각 속성(feature)들의 계수를 구할 수 있다. 이 때 각 계수(coefficients)들은 데이터를 분류함에 있어 해당 속성이 얼마나 중요한지 해석하는 데에 사용할 수 있다.